最近は本業でデータ分析を行うことが多くなり、データサイエンス全般にもっと詳しくなりたいと思っている私です。
少し前から統計検定準1級の勉強をぼちぼち始めました。
統計検定準1級の公式テキストでは「収束」の概念の説明とその種類が多く出てくるのですが、その説明が難解で、
数回読んだくらいでは意味がよく理解できません。
概収束、確率収束、平均収束、平均二乗収束など、たくさんの収束があるのですが、
それぞれの定義の違いを理解できたと思えるようになるまでにかなり時間がかかりました。
しかし長時間理解しようと努めた結果、自分なりにわかりやすい説明の仕方を思いついたので、
ここで収束の種類とその特性をなるべく分かりやすく説明したいと思います。
収束の種類の理解に手間取っている方の参考に少しでもなれば幸いです。
前提
収束を説明する時、多くのテキストではその数式を元に定義の説明をしているのですが
いきなり数式を出されても多くの人はすぐに理解できないと思います。
こういった概念的な要素の強い話では、いくら数式や定義をそれらしく説明しても
具体例がなければ腑に落ちるレベルの理解までは到達できないと思います。
そこでこの記事では、収束の概念の説明に具体例を積極的に使いたいのですが
その具体例で使う用語の説明を、ここでしておきたいと思います。
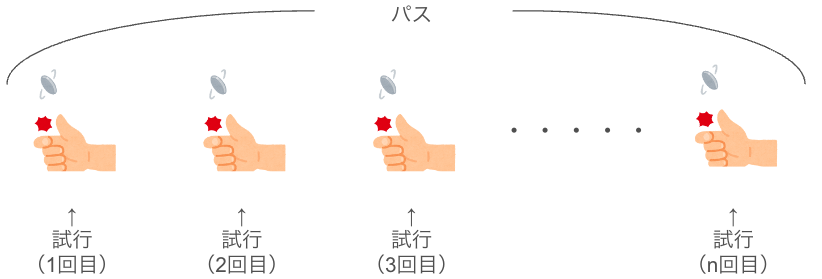
例えば、Aさんがあるコインをn回投げるとします。
この時、コインを投げる一回一回の行為を「試行」と呼びます。
つまりAさんは、コインを投げるという「試行」をn回繰り返します。
そして、このコインをn回投げる、一連の試行の集合のことを「パス」と呼びます。
概収束
概収束(almost sure convergence)とは、他の収束に比べて最も強い収束の概念です。
一応数式を載せておくと、以下のようになります。
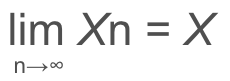
定義を説明すると、「nが無限大に近づくと、Xn が X に収束する確率が1である」と言えます。
先ほどのコインを投げる例で言うと、
コインを投げる度に、投げた結果のうち表が出た割合が1/2に近づいていくというようなケースです。
概収束のミソは、ほぼすべてのパスで収束先に収束していくということです。
例えばコインをn回投げる、という行為(パス)をAさん、Bさん、Cさん、その他大勢が1人1パス行うとします。
この時概収束では、すべての人のパスが収束していきます。
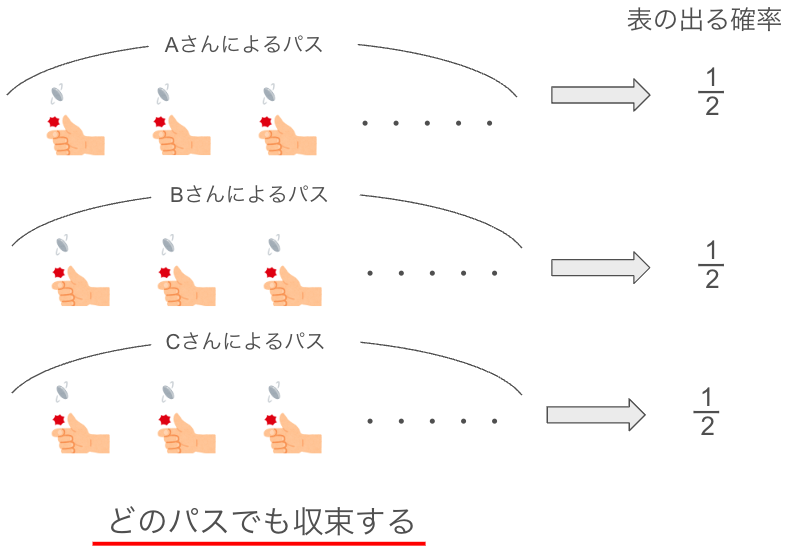
このように、パス単位で確実に収束していく、とても強く安定性の高い収束が概収束です。
確率収束
確率収束(convergence in probability)は、
パスの回数を増やすたびに、パスが収束先に収束する確率がどんどん高くなっていくことを意味します。
式は以下のようになります。
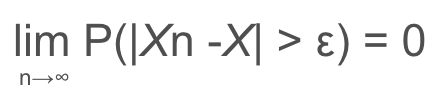
定義を説明すると、
「0よりも大きい任意のεに対して Xn と X(収束先)が異なる確率が0に近付いていく」 となります。
コインを投げる例で言えば、
パスごとに得られる「表の出る割合」が 1/2 に収束する確率が、パスの数が増えるごとに高くなっていきます。
たくさんのパスを繰り返すと、ほとんどのパスで表の割合が 1/2 に近づく確率が増す、というイメージです。
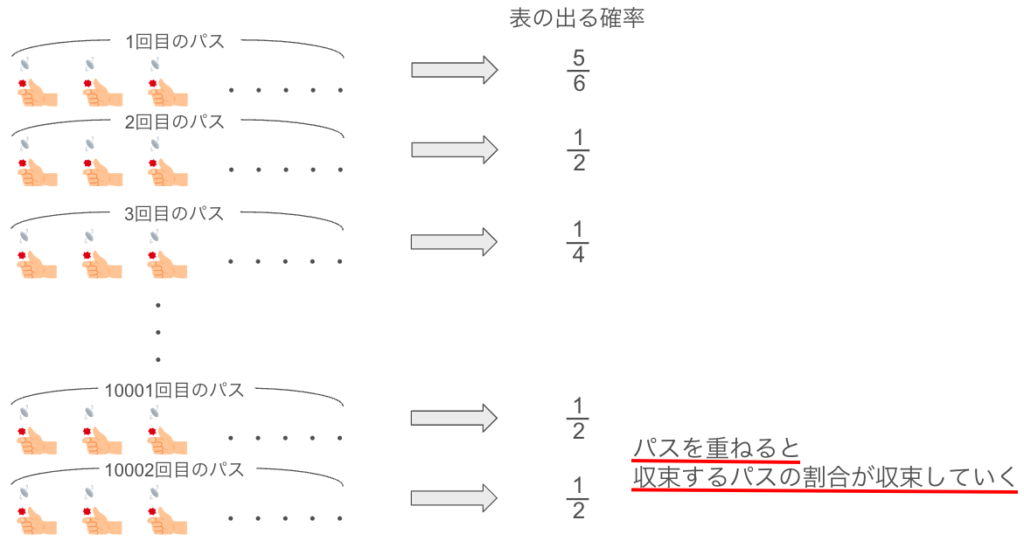
概収束とは違って、ひとつひとつのパスが必ずしも収束するとは限りません。
故に確率収束は、概収束よりも弱い収束となります。
平均収束
平均収束(mean convergence)とは、
複数のパス全体の期待値(平均)が収束先に向かっていることを指します。
数式で言うと以下のようになります。
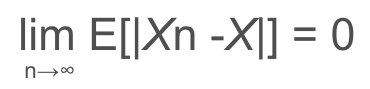
概収束などとは違って、
パスひとつひとつでは必ずしも収束先に収束する必要はありません。
パス全体の平均値が収束先に向かえば、それを平均収束と言います。
コイン投げの例で言うと、
例えば表の出る確率がパス1で1/4、パス2で3/4、パス3で1/6、パス4で5/6に収束した場合、
パスごとに見れば1/2に収束していないですが
パスの平均(期待値)は1/2となります。つまり平均収束しています。
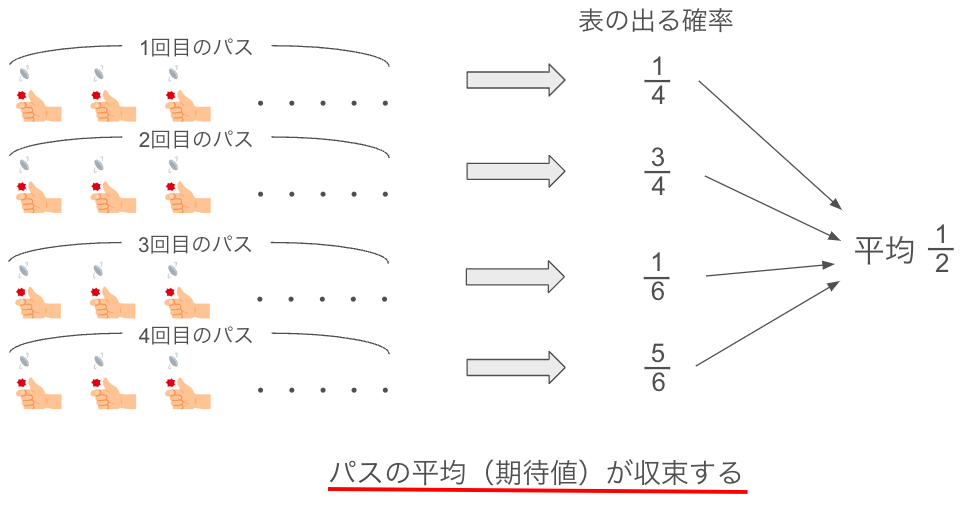
このように、パス単位では必ずしも収束しないが、パスの平均を取れば収束することを平均収束と言います。
概収束はパス1つで収束し、確率収束はパスを重ねれば収束するパスが増えていくのでした。
一方、平均収束はパス単位で収束しているかどうかは問題ではありません。
そのため、平均収束は概収束、確率収束よりも弱い収束となります。
平均二乗収束
平均二乗収束(mean square convergence)は、平均収束に似た概念です。
実際の値と収束先の値の差(誤差)の2乗の期待値が0に収束していきます。
数式は以下のようになります。
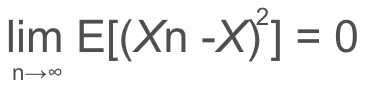
平均収束の式に2乗が追加されているだけです。
基本的な概念は平均収束と同じなのですが、
Xn と収束先の値( X )の差(つまり誤差)を2乗しているが故に、収束値からの少しの誤差でも値が強調されてしまいます。
そのため、この誤差の2乗が0に近づいていくには、平均収束よりも、より強く素早い、安定した収束が求められます。
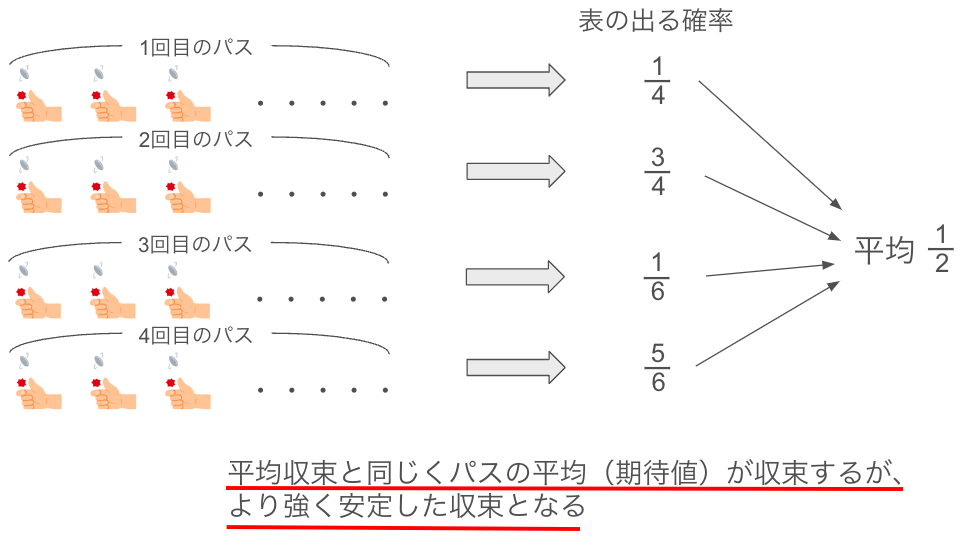
パスを重ねるごとにパスの平均値が収束先に収束していくという点では、平均収束と平均二乗収束は共通しています。
ただし、平均二乗収束の方が、ここのパスのばらつきが少なく、安定的に収束していきます。
誤差の値よりも、その二乗の方が当然値は大きくなるので、
誤差を0にするのと、誤差の2乗を0にするのとでは、当然後者の方が強く収束することが求められるわけです。
よって平均二乗収束は、平均収束よりも強い収束となります。


コメント